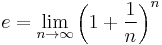Jacob Bernoulli

Jacob Bernoulli

Jacob Bernoulli
Born 27 December 1654(1654-12-27)
Basel, Switzerland
Died 16 August 1705(1705-08-16) (aged 50)
Basel, Switzerland
Residence Switzerland
Nationality Swiss
Fields Mathematician
Institutions University of Basel
Alma mater University of Basel
Doctoral students Johann Bernoulli
Jacob Hermann
Nicolaus I Bernoulli
Known for Bernoulli differential equation
Bernoulli numbers
(Bernoulli's formula
Bernoulli polynomials
Bernoulli map)
Bernoulli trial
(Bernoulli process
Bernoulli scheme
Bernoulli operator
Hidden Bernoulli model
Bernoulli sampling
Bernoulli distribution
Bernoulli random variable
Bernoulli's Golden Theorem)
Bernoulli's inequality
Lemniscate of Bernoulli
Notes
Brother of Johann Bernoulli.
For other family members named Jacob, see Bernoulli family.

Jacob Bernoulli (also known as James or Jacques) (27 December 1654 – 16 August 1705) was one of the many prominent mathematicians in the Bernoulli family.

Jacob Bernoulli was born in Basel, Switzerland. Following his father's wish, he studied theology and entered the ministry. But contrary to the desires of his parents, he also studied mathematics and astronomy. He traveled throughout Europe from 1676 to 1682, learning about the latest discoveries in mathematics and the sciences. This included the work of Robert Boyle and Robert Hooke.

He became familiar with calculus through a correspondence with Gottfried Leibniz, then collaborated with his brother Johann on various applications, notably publishing papers on transcendental curves (1696) and isoperimetry (1700, 1701). In 1690, Jacob Bernoulli became the first person to develop the technique for solving separable differential equations.

Upon returning to Basel in 1682, he founded a school for mathematics and the sciences. He was appointed professor of mathematics at the University of Basel in 1687, remaining in this position for the rest of his life.

Contents

Important works

Jacob Bernoulli is best known for the work Ars Conjectandi (The Art of Conjecture), published eight years after his death in 1713 by his nephew Nicholas. In this work, he described the known results in probability theory and in enumeration, often providing alternative proofs of known results. This work also includes the application of probability theory to games of chance and his introduction of the theorem known as the law of large numbers. The terms Bernoulli trial and Bernoulli numbers result from this work. The lunar crater Bernoulli is also named after him jointly with his brother Johann.

Discovery of the mathematical constant e

Bernoulli discovered the constant e by studying a question about compound interest which required him to find the value of the following expression (which is in fact e):

e = \lim_{n\to\infty} \left( 1 %2B \frac{1}{n} \right)^n

One example is an account that starts with $1.00 and pays 100 percent interest per year. If the interest is credited once, at the end of the year, the value is $2.00; but if the interest is computed and added twice in the year, the $1 is multiplied by 1.5 twice, yielding $1.00×1.5² = $2.25. Compounding quarterly yields $1.00×1.254 = $2.4414..., and compounding monthly yields $1.00×(1.0833...)12 = $2.613035....

Bernoulli noticed that this sequence approaches a limit (the force of interest) for more and smaller compounding intervals. Compounding weekly yields $2.692597..., while compounding daily yields $2.714567..., just two cents more. Using n as the number of compounding intervals, with interest of 100%/n in each interval, the limit for large n is the number that came to be known as e; with continuous compounding, the account value will reach $2.7182818.... More generally, an account that starts at $1, and yields (1+R) dollars at simple interest, will yield eR dollars with continuous compounding.

Personal Life

Bernoulli chose a figure of a logarithmic spiral and the motto Eadem mutata resurgo ("Changed and yet the same, I rise again") for his gravestone; the spiral executed by the stonemasons was, however, an Archimedean spiral.,[1] “[Jacques Bernoulli] wrote that the logarithmic spiral ‘may be used as a symbol, either of fortitude and constancy in adversity, or of the human body, which after all its changes, even after death, will be restored to its exact and perfect self’.” (Livio 2002: 116).

Jacob had daughter and son.

References

  1. ^ Jacob (Jacques) Bernoulli, The MacTutor History of Mathematics archive, School of Mathematics and Statistics, University of St Andrews, UK.

Further reading

External links

Bernoulli family tree
 
 
 
 
 
 
 
 
 Nicolaus Bernoulli
(1623–1708)
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
Jacob Bernoulli
(1654–1705)
 
 Nicolaus Bernoulli
(1662–1716)
 
 
 
 Johann Bernoulli
(1667–1748)
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 Nicolaus I Bernoulli
(1687–1759)
 
 Nicolaus II Bernoulli
(1695–1726)
 
 Daniel Bernoulli
(1700–1782)
 
 Johann II Bernoulli
(1710–1790)
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 Johann III Bernoulli
(1744–1807)
 
 Daniel II Bernoulli
(1751–1834)
 
 Nicolaus IV Bernoulli
(1754–1841)
 
 Jakob II Bernoulli
(1759–1789)
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 Nicolaus
(1793–1876)
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 Fritz
(1824–1913)
 
 Theodor
(1837–1909)
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 Hermann Hesse
(1877–1962)
 
 Maria Bernoulli
(1868–1963)
 
 Hans Benno Bernoulli
(1876–1959)
 
Family tree of the Bernoulli family